**正比例函数的一線三直角應用(八年級數學)**

**引言**
在八年級數學正比例函數的學習中,其應用最基本的便是求解析式。根據其特點,我們只需要得知直線上的某一點坐標,即可求得比例係數 (k) 。而於坐標系中求點坐標,我們在七年級已建立了坐標與幾何線段之間的聯繫。對於初次經歷數形結合的八年級學生而言,這需要一個熟練的過程。換句話說,一般會通過作垂線於坐標軸的方式,完成坐標與線段長度的轉換。同時,需要留意的是,坐標是有符號區別的,而線段長度卻是正數。須辨別點位於哪一個象限。
**題目**
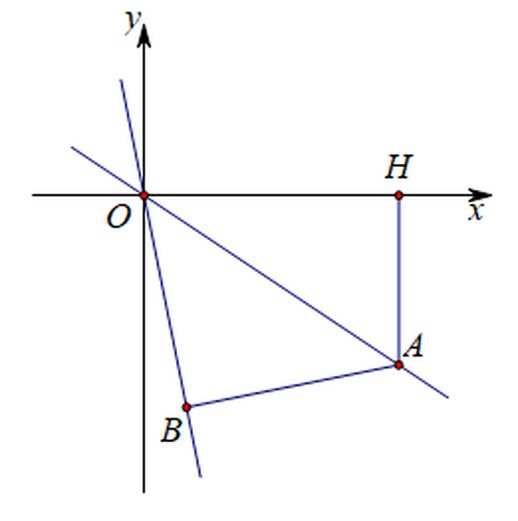
圖中,正比例函數 (y = kx) 經過點 (A) 。點 (A) 位於第四象限,且過點 (A) 作 (AH perp x) 軸,垂足為點 (H) 。點 (A) 的橫坐標為 (3) ,且正三角形 (AOH) 的面積為 (3) 。
(1)求正比例函數的解析式;
(2)若直線 (y = mx) ((m < k))上有一點 (B) 滿足 ∠AOB = 45°,且 (OB = AB) ,求 (m) 的值。
**解析**
(1)此正比例函數經過點 (A) ,因此我們需要求出點 (A) 的坐標。其橫坐標已給定為 (3) ,縱坐標則隱藏在正三角形 (AOH) 面積為 (3) 的條件中。正三角形 (AOH) 是直角三角形,面積等於 (OH) 與 (AH) 乘積的一半。其中 (OH) 為 (3) ,因此可以求出 (AH) 為 (2) 。點 (A) 的坐標為 ((3, -2)) 。再將其代入 (y = kx) 中可得 (k = -2/3) 。正比例函數的解析式為 (y = -2/3x) ;
(2)當我們看到 ∠AOB = 45° 時,八年級解題經驗中最容易聯想到的是等腰直角三角形。恰好有這樣一個特殊銳角。那麼,圖中的 △AOB 是否符合這樣的條件呢?
結合題目中的條件,(OB = AB) ,答案肯定。△AOB 是個等腰直角三角形。這就形成了 “一线三直角” 最基本的條件。其構造方法是,過點 (B) 向 (y) 軸作垂線,如下圖:
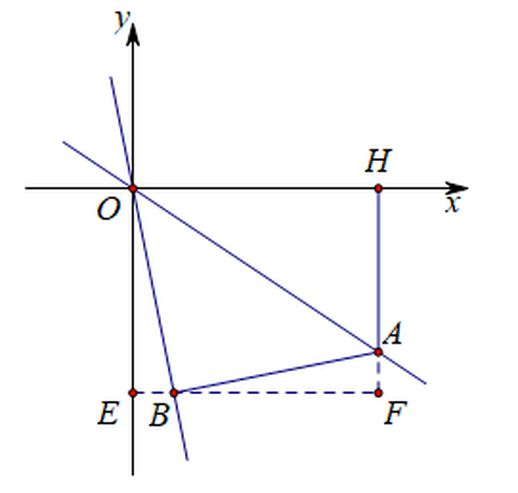
圖中 △OBE 與 △BAF 的全等條件很容易找到:∠BEO = ∠F = 90°。利用同角的餘角相等,證明∠ABE = ∠BAF,再結合 (OB = AB) ,得到 △OBE ≌ △BAF,所以 (BE = AF) ,(OE = BF) 。請注意,我們需要知道 (BE) 和 (OE) 的長度,分別對應求點 (B) 的橫縱坐標,因此需要找出它們之間的等量關係。圖中四邊形 (OEFH) 可證明為一個矩形,因此 (EF = OH = 3) ,而 (OE = HF) 。以下進行替換:
(OE = AH + AF = 2 + AF = 2 + BE) ,
另一方面:
(BF = EF – BE = OH – BE = 3 – BE) 。
我們可以得到方程式 (2 + BE = 3 – BE) ,可求出 (BE = 1/2) 。由此得到 (OE = 5/2) 。至此得到點 (B) 的坐標為 ((1/2, -5/2)) 。将其代入 (y = mx) ,求出 (m =-5) 。
**解題反思**
此題作为一道正比例函数习题课的思考题布置下去,交上来的同学很少,对于刚刚学完正比例函数的八年级学生而言,综合力度较大,完成不易,但借助这道题,至少让学生明白正比例函数的直线特征与几何里是完全一样的,只是在坐标系中,几何中的直线可以用解析式表示,即几何代数化,为后面一次函数的应用发一个“预告片”,能从这道题反思自己思路缺陷的学生,无疑将在后续学习中如鱼得水。