**一元二次方程的起源**
一元二次方程的历史可以追溯到古希腊时期,当时一些学者就对其进行了探索。著名的数学家欧几里得提出了用几何方法求解二次方程的方法。
一元三次方程的重大突破
意大利数学家斯卡拉穆奇(Scipione del Ferro)在16世纪发现了求解一元二次方程的通式,并传授给了他的学生费拉里。费拉里在此基础上进一步研究,推导出一元三次方程的通式,并提出了求解四次方程的方法,这些成果被誉为“费拉里解法”。
代数符号的运用
法国数学家笛卡尔在17世纪利用代数符号对二次方程进行了统一的表示,并建立了代数几何学理论。他还使用解析几何的方法揭示了一元二次方程的几何意义,为代数和几何之间的关系奠定了基础。
二次方程通式的发现
到了18世纪,欧拉和拉格朗日分别发现了二次方程的通式,称为“欧拉公式”和“拉格朗日公式”。这些公式不仅提供了方程解的具体表达式,而且有助于研究方程根的性质和关联,对代数学的进步做出了显著贡献。
一元二次方程的对称性
一元二次方程的形式为:
其通解为:
这个通解隐藏着一个重要的性质——对称性。对称性极大地简化了求解一元二次方程的过程,而缺乏对称性正是导致求解一元三次方程难度极高的原因。求解三次方程如此之难,以至于16世纪的数学家穷尽一生也未能找到其通解。
求解方程是数学的基础技能。我们首先学习求解最基本的方程:f(x)=0。这类方程的解有时被称为函数的“零点”或“根”。在我们逐一找出二次方程的根之前,先从一个简单的例子入手:f(x)=x^2−9 的根是什么?只需解方程 f(x)=0 即可。
这非常简单,也容易验证。注意最后一行中的正负号,这也说明了二次方程的对称性。如果你想象这两个解在数轴上的位置,你会发现它们关于x=0对称。
回想一下,二次函数的图像是一个抛物线,每条抛物线都有一个对称轴,将抛物线分成两个镜像部分。在这个例子中,对称轴是y轴,
可以看到它的两个根在x轴上,与y轴的距离相等。
对于稍微复杂一些的二次方程,比如
求它的根就稍微繁琐一点,
我们可以将 f(x) 设为 0,把 9 移到右边,但我们不能对两边同时开平方根来分离 x,因为含有 x 的另一个项阻碍了这个操作。这个函数具有对称性,我们可以利用这种对称性绕过这个问题,只需进行一些代数运算,使对称性更加明显。将函数改写为
现在关注 x(x−8) 这部分,当 x = 0 或 x = 8 时,这部分将等于 0,这保证了 f(0) 和 f(8) 取相同的值 -9。这为我们提供了抛物线上两个对称的点,由于对称轴必定把 x=0 和 x=8 均分,所以对称轴一定是直线 x=4。
现在我们已经发现了对称性,我们可以利用它来解决问题。我们需要将抛物线向左移动四个单位,这样对称轴就能从直线 x=4 移动到直线 x=0。为了实现这种平移,我们可以使用一种简单的代数方法:将 x**替换为 x+4**。
我们把 x 替换成 x + 4,得到一个新的二次函数,记为 g(x)。换句话说,令 g(x) = f(x + 4)。观察一下当我们化简 g(x) 时会发生什么:
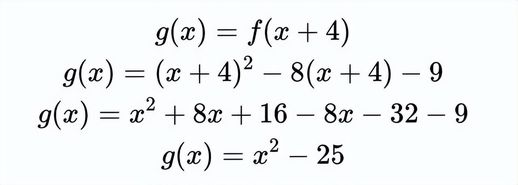
经过应用分配律和合并同类项,新二次函数的 x 项消失了,这使得求解 g(x) 的根变得容易:
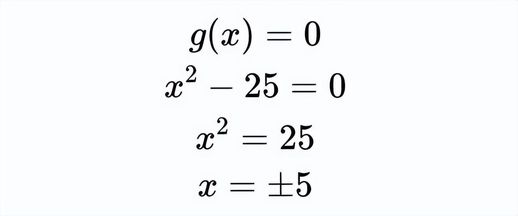
g(x) 的根是 x = ±5,所以为了求 f(x) 的根,我们只需要将 g(x) 的根向右平移四个单位即可。这样就得到了 f(x) 的根:4 ± 5,即 9 和 -1,你可以通过计算 f(9) = f(-1) = 0 来验证这一点。
解决这个稍微困难的二次方程的关键是将它**平移并消除干扰的 x 项**,从而将其转化为一个更容易求解的二次方程。这种方法适用于任何二次函数。对于任意给定的二次函数 f(x) = ax^2 + bx + c,你总是可以用同样的分解方法找到它的对称轴:
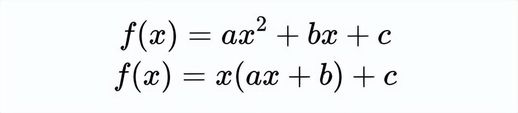
通过这个公式,你可以看到 f(0) = f(-b/a) = c,这意味着对称轴位于 x = 0 和 x = -b/a 之间的中点上。换句话说,任何二次函数 f(x) = ax^2 + bx + c 的对称轴都是直线 x = -b/2a。这应该很熟悉,因为它隐藏在二次方程的求根公式中!
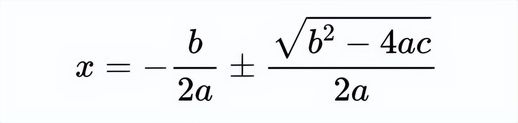
二次方程公式的基础在于二次方程的根关于 x=−b/2a 对称。你可以利用这种对称性来求根:只需将 f(x) 平移 −b/2a 即可。这会消除 x 项,从而可以轻松地分离 x 并解出方程。它展示了重要代数和几何之间的联系。
通过对称性解二次方程可能会激发我们尝试在三次方程上使用类似的方法。尽管三次方程确实具有对称性,但这种对称性无法帮助我们解像 f(x)=0 这样的方程。三次函数的图像具有“中心对称性”,这意味着每个三次函数图像上都有一个特殊的点,如果一條直线通过该点并在其他任何地方与三次函数图像相交,则它再次在该点对称相交。
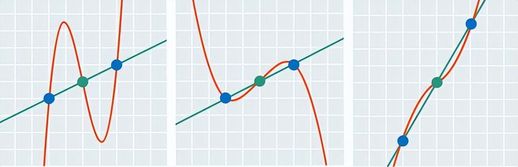
这种对称性非常有力,但它对于寻找函数的根没有帮助。因为函数的根出现在其图像与水平线 y=0(即 x 轴)相交的位置,而一般情况下,这些交点不会对称于三次函数的特殊对称点。
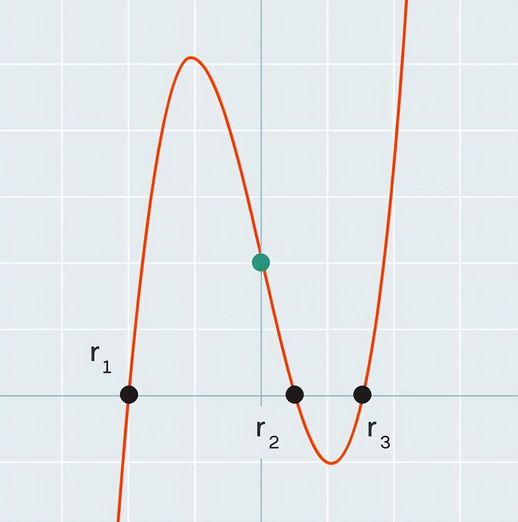
事实上,三次函数也可能只有1个根。没有对称性可言。
关于二次方程的一些东西可以帮助我们。
如果有一个二次函数 f(x) = ax^2 + bx + c,并且已知它的根为 r1和 r2,那么我们总是可以把 f(x)写成“因式分解”的形式:
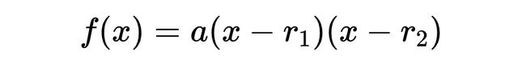
现在,当我们将其展开并化简后,得到的结果非常有用,方便我们进一步研究该函数。
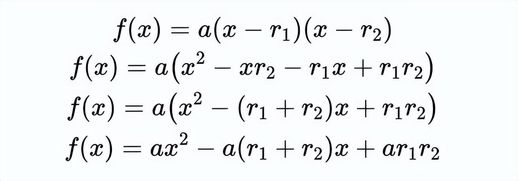
请注意,二次函数中 x 项的系数涉及两个根 r_1 和 r_2 的和。这是韦达定理之一的关键:给定一个二次函数 f(x) = ax^2 + bx + c,其两个根的和将始终为 -b/a。你可以通过将二次函数的一般形式设置为因式分解形式
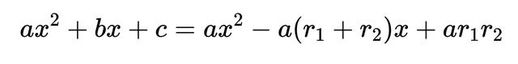
并观察只有当它们对应的系数相两个多项式才可以实际上是相同的。在这种情况下,这意味着方程两侧的 x 项系数必须相等,因此我们可以将它写成:
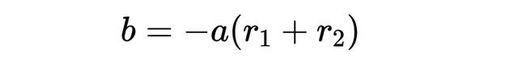
整理得到,
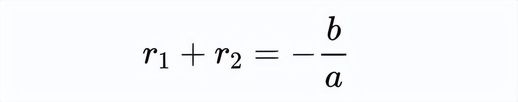
请注意,将该方程的两侧同时除以2可以证明一个有趣的结论:二次函数的两个根的平均值等于对称轴的x值:
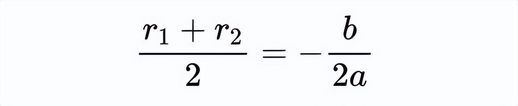
通过将对称轴从 x=−b/2a 移动到 x=0 来平移这个抛物线,也会将两个根的平均值从 −b/2a 改变为 0。
但如果根的平均值是0,那么根的和也一定是0,并且两个根的和以二次方的因式形式出现:
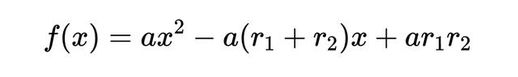
这意味着将二次函数进行平移,使其两个根的和为0,也会使x项消失。这正是帮助我们解决早期的二次方程的方法,而对于三次函数的根,也有类似的结果。
给定一个三次函数,
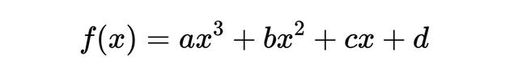
我们可以像解二次方程一样,对三次方程进行因式分解。如果三次方程有根r1,r2,r3,我们可以将三次函数写成它的因式形式:

乘出来得到,

然后我们让它等于一般形式。由于相应的系数必须相同,我们最终得到了韦达的三次方根和公式:

我们可以在方程两边同时除以3得到
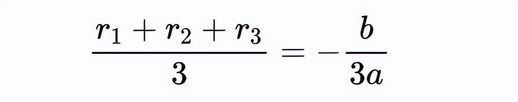
这告诉我们,三次函数的根的平均值是−b/3a。现在,如果我们将这个三次函数向左平移这个量,那么它的平均根将变为0,这将使得三个根的和等于0,进而使得在我们平移后的三次函数中x^2的系数消失。
简而言之,通过变换 g(x)=f(x−b/3a) 会得到一个所谓的“降阶”三次函数,这意味着它没有 x^2 一项。我们变换后的降阶三次函数将看起来像这样:

可以通过原始三次函数的 a、b、c 和 d 表达出系数 m 和 n,但这些系数的具体值并不那么重要。更重要的是,有一些保证能够找到降阶三次函数根的技巧。实际上,这样的技巧是16世纪卡尔达诺和塔尔塔利亚之间争执的核心。这是一个漫长而引人入胜的故事,其引人注目的数学结论是:将任何三次方程转化为降阶三次方程的能力,以及解任何降阶三次方程的能力,使我们能够解每个三次方程。

这是三次求根公式,和二次公式一样,可以解所有的三次方程。但与二次公式不同的是,它看起来非常繁琐。